Сага об икосаэдре. Моисеев Д.И.
Предлагаемая книга является результатом оригинальных исследований автора в области построения моделей разнообразных кристаллических структур неживой и живой природы, включая такие открытия 25-летней давности как квазикристаллы, фуллерены и нанотрубки. Установлено, что икосаэдр может осуществлять, кроме собственно икосаэдрических связей, функции тетраэдра и октаэдра при построении моделей кристаллических структур. Это позволяет предположить, что икосаэдр является, в структурном смысле, универсальным многогранником, о чём свидетельствуют созданные модели.Книга относится к области научно-популярной литературы. Основная её часть посвящена популярному изложению рассматриваемых вопросов, а все математические выкладки оформлены в виде приложений.
САГА ОБ ИКОСАЭДРЕ
ВВЕДЕНИЕ
"Природа! Из простейшего вещества творит она противоположнейшие произведения, без малейшего усилия, с величайшим совершенством, и на всё кладёт какое-то нежное покрывало. У каждого её создания особенная сущность, у каждого явления отдельное понятие, а всё едино".
Иоганн Вольфганг Гёте
Человека всегда поражало и восхищало совершенство окружающего мира. Всё, что производит природа, соразмеряется законом гармонии. Уже в Древней Греции, у пифагорейцев, родилось представление о том, что гармония является основой прекрасного. Изучение её законов стало важной частью познания природы. Назначение и цель гармонии – упорядочить части, в некотором смысле различные, так, чтобы они одна другой соответствовали, создавая красоту.
Гармонии обязательно сопутствует симметрия. Издавна в своих творениях люди предпочитают правильные геометрические формы – квадрат, круг, равнобедренный треугольник, пирамиду и т. д. Симметричные фигуры обычно предпочтительнее, чем несимметричные.
В.И. Вернадский в своей книге "Химическое строение биосферы Земли и её окружения" писал: "…чувство симметрии и реальное стремление его выразить в быту и в жизни существовало в человечестве с палеолита или даже с эолита, т.е. с самых длительных периодов в доистории человечества. Симметрия явно проявляется в строении человеческого тела. Она же присутствует в гармонии человеческих движений, как в танцах, так и в технической работе, где проявляется геометрическая закономерность".
У пифагорейцев слово "симметрия" выражало соразмерность, пропорциональность, одинаковость в расположении частей, понималось как способ согласования многих частей, с помощью которого они объединяются в целое; симметрия, в самом широком смысле, противоречит хаосу, беспорядку.
Симметрия – настолько широко распространённое явление в природе, среди предметов обихода, в произведениях искусства, что понятие о симметрии, хотя и недостаточно осознанное, воспринимается нами с детства. Особенно разнообразно проявляется симметрия в царстве живой природы.
В нашей повседневной жизни симметрия обычно ассоциируется с зеркальным отражением. Таковы, например, правая и левая половины нашего тела. Но на самом деле такая симметрия не является в строгом смысле зеркальной: правая и левая половины человеческого тела асимметричны с точки зрения расположения внутренних органов. И даже во внешнем облике человека присутствует некоторая асимметрия. Мы привыкли отождествлять себя с собственным отражением в зеркале, где правая и левая стороны нашего лица меняются местами. Поэтому нам трудно иногда найти в фотоателье свою фотографию, на которой мы выглядим так, как видят нас окружающие, и фотоаппарат в том числе. Всё дело в некоторой асимметрии нашего лица, хотя эта неодинаковость правой и левой части может придавать нашему облику определённую живость, и даже некоторый шарм. Вспомним скульптурные изображения древнегреческих богинь: их лица безжизненны именно потому, что ваятель сделал их совершенно симметричными. В биологии симметрию живых организмов называют билатеральной (двусторонней), и в этом, быть может, кроется обобщённая трактовка законов симметрии.Многолетние исследования математиков и натуралистов привели к более широкой оценке понятия симметрии – это неизменность формы (структуры) какого-либо объекта по отношению к определённым преобразованиям, выполняемым над ним.
Характерной особенностью использования понятия симметрии в современной физике является его весьма абстрактный характер, зачастую очень далёкий от наглядности. Если для кристаллографической симметрии не представляло никакого труда построить наглядные образы симметричных предметов, то в современной науке центральным пунктом содержания понятия симметрии становится не "симметричная вещь", а преобразование (операция) симметрии, которую понимают как неизменность (инвариантность) любого свойства при некоторых преобразованиях. Часто термины "симметрия" и "инвариантность" употребляются как синонимы, по крайней мере, в физической литературе, где они обозначают "свойство оставаться неизменным относительно одной или нескольких различных операций".
Д.А. Франк-Каменецкий утверждает, что "…принципы инвариантности отражают общие свойства пространства, а не находящихся в нём тел, в то время как симметрия – это свойство конкретных частиц, а не общие свойства пространства". Поэтому "инвариантность" можно расценивать как некоторое расширение понятия "симметрия".
Более подробно сведения о кристаллографической симметрии, необходимые и достаточные для понимания существа дела, будут рассмотрены в соответствующей главе. Нам предстоит также посетить мир многогранников, дать им необходимую оценку с позиций моделирования кристаллических структур и выбрать рациональные структурные элементы.
Рассматривая многогранники, невозможно обойти молчанием икосаэдро-додекаэдрическую доктрину, подкреплённую в последние десятилетия многочисленными фактами, но и приобретшую новых противников. В связи с этим вполне естественно обратиться к такому важному понятию как "золотая пропорция" и определить её место в ряду мировоззренческих категорий.
После всех этих ознакомительных глав можно, наконец, приступить к построению моделей разнообразных кристаллических структур неживой и живой природы, охватив такие открытия 25-летней давности как квазикристаллы, фуллерены и нанотрубки. Определённый интерес представляют и модели структур на основе так называемых "минералогических икосаэдров", несколько деформированных по сравнению с правильными многогранниками.
Сравнительная оценка представленных моделей позволяет осуществить их классификацию и сформулировать некоторые предположения относительно значимости икосаэдра как универсального элемента моделирования кристаллических структур.
МОДЕЛИРОВАНИЕ МОЛЕКУЛЯРНЫХ СТРУКТУР
"Наглядное понимание играет первенствующую роль в геометрии, и притом не только как обладающее большей доказательной силой при исследовании, но и для понимания и оценки результатов исследования".
Д. Гильберт
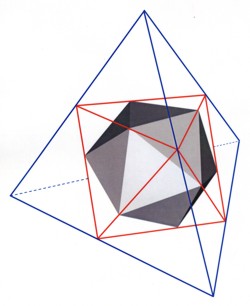
Итак, икосаэдр в наших моделях будет символизировать молекулу, а октаэдр – связь между молекулами. Следуя принципу закономерно, симметрично и целесообразно построенных ассоциаций, необходимо выбрать такие взаимные направления связей каждого икосаэдра, которые соответствовали бы расположению граней тетраэдра, или октаэдра, или икосаэдра. Как было показано в главе 4, икосаэдр способен выполнять все эти роли. При этом, с учётом того, что грань икосаэдра развёрнута по отношению к граням совмещённых с ним тетраэдра и октаэдра (Рис.26), в некоторых случаях возможен как "правый", так и "левый" вариант расположения связей.
Следует обратить внимание на "собираемость" (выполнимость) всех представленных далее моделей. Несмотря на неизбежные погрешности, сопутствующие изготовлению многогранников и их сборке, никаких трудностей при создании сложных конструкций на основе этих многогранников не возникало. Конечно, можно привести геометрические доказательства этой "собираемости", но это перегрузило бы содержание книги громоздкими математическими выкладками. В тех случаях, когда автор считал такие доказательства необходимыми, они вынесены в Приложения.
На Фото показаны два варианта возможных тетраэдрических связей икосаэдра – правый (D) и левый (L)
Эти конструкции являются зеркальными двойниками. Если их объединить, они как бы нейтрализуют друг друга, и получается симметричная схема с восемью возможными направлениями связей (см.фото ). Присмотревшись к этому варианту, нетрудно убедиться в том, что он соответствует октаэдрическим связям икосаэдра.
Все остальные сочетания направлений связей, не укладывающиеся в тетраэдрическую или октаэдрическую схему, будем считать икосаэдрическими. Очевидно, что максимальное число таких связей равно 20-и, по числу граней икосаэдра.
Из факта великого разнообразия реальных молекул в природе следует, что столь же велико количество возможных сочетаний межмолекулярных связей.
При моделировании молекулярных структур следует допустить частичное использование всех разрешённых направлений связей, предполагая, что в процессе формирования молекулярных ассоциаций могут участвовать молекулы различных сортов.
Читаем у Д. Дж. Бернала (в статье за 1968 г.): "Соединение молекулы с молекулами того же типа может иметь место в различных измерениях. Если укладка одномерная, мы имеем линейный полимер, прямолинейный или спиральный; если она двумерная – поверхностную молекулу, которая может быть плоской, цилиндрически свёрнутой или замкнутой поверхностью (глобулярной). Только в том случае, если укладка регулярна в трёх измерениях, мы будем говорить о решёточной структуре истинного кристалла. …Мы привыкли к классическому различению между атомами и молекулами. Наступило время, когда мы должны создать новые виды различия, учитывающие более высокие степени агрегатирования, возможные не только для отдельных атомов, но и для групп атомов и молекул первого уровня; этот процесс может быть распространён и далее и может охватывать макромолекулы второго, третьего и четвёртого уровней агрегатирования". Далее будем придерживаться этой терминологии.
В ПОИСКАХ МОДЕЛИ КВАЗИКРИСТАЛЛА
Практически все известные на данный момент квазикристаллы – это металлические сплавы. Но симметрийные свойства квазикристаллов обладают универсальностью. Можно предположить, что с большой вероятностью такие структуры существуют и в мире живой природы, обладающей огромным разнообразием форм. Поэтому икосаэдр, используемый при создании наших моделей, может символизировать как молекулу, так и атом. Существо дела от этого не меняется, поскольку речь идёт о построении геометрических образов возможных структур независимо от их принадлежности к живой или неживой материи.
Чтобы понять, пригодны ли наши модели второго и третьего уровней агрегатирования для построения модели квазикристалла, необходимо оценить их метрические параметры. Обратимся к Приложению 5, из которого следует, что в нашем распоряжении имеется два ромба (ромб 1 и ромб 2), которые незначительно отличаются от ромбов Пенроуза величиной угла при вершине ромба. Кроме того есть блок ромб 3, совпадающий с "толстым" ромбом Пенроуза по углу при вершине, но отличающийся от него по форме. Именно с блока ромб 3 начнём строительство моделей квазикристаллических структур, поскольку этот блок буквально пронизан золотой пропорцией.
На Фото представлена модель, очень похожая на паркет Пенроуза, в отличие от которого она выполнена с использованием одного многоугольника. Это замощение не является периодическим – оно, очевидно, не переходит в себя ни при каких сдвигах, но его конечная часть (ромб 3) встречается во всём замощении бесчисленное множество раз (дальний ориентационный порядок). Кроме того, вся структура обладает осью симметрии 5-го порядка, в то время как таких осей у периодических замощений не существует.
Попытаемся всё-таки пойти по стопам Пенроуза и построить паркет с использованием блоков ромб 1 и ромб 2. В результате возникает модель, показанная на Фото:
В центральной точке этой структуры сопрягаются 5 блоков ромб 2, сумма вершинных углов которых составляет ~3550 < 3600. В результате формируется пятигранная пирамидальная поверхность, простирающаяся в бесконечность. На этой поверхности выстроен паркет из блоков ромб 1 и ромб 2 Они не имеют общих внутренних точек, и между ними нет промежутков. Расположим эту конструкцию так, чтобы оси, проходящие через противолежащие вершины икосаэдров, были перпендикулярны плоскости страницы (вспомним, что в любой нашей сборке все икосаэдры ориентированы одинаково) – Фото. Получаем проекцию пирамиды на плоскость страницы. Вследствие наклона ромбов их проекции приобретают новые значения вершинных углов. Очевидно, что эти значения составляют 720 – для проекции ромба 2 и 360 – для проекции ромба 1. Другими словами, проекция нашей пирамидальной поверхности на плоскость страницы даёт один из возможных вариантов паркета Пенроуза. И, наоборот, построенная модель представляет собой проекцию паркета Пенроуза на пятигранную пирамидальную поверхность с углом при вершине ~71.
Если остановиться на некотором шаге формирования пирамиды с основанием в виде пентагона, то из 12-ти таких пирамид может быть построена глобулярная поверхностная структура в форме пентагондодекаэдра (Фото 52a). На фотографии – вид изнутри на половину этой конструкции, состоящую из шести пирамид. Здесь как бы стирается грань между моделями поверхностных структур, рассмотренными ранее, и моделями квазипериодических структур, подобных паркетам Пенроуза. Дополнительным тому подтверждением является тот факт, что полученная модель легко сопрягается с поверхностными структурами, представленными на Фото 42 и Фото 43. Результат такого сопряжения показан на Фото 52b и Фото 52c.
52b
52c
ЗАКЛЮЧЕНИЕ
Мы Провидению доверим свой покой,
Которое своей невидимой рукой
Незримо бережёт червя и человека
И движет атомы и целые миры".
Н.М. Карамзин
Опыт моделирования кристаллических структур на основе икосаэдра подтверждает факт универсальности этого многогранника. Все построенные структуры базируются на весьма ограниченном количестве моделей макромолекул второго уровня: ромб 1, ромб 2, ромб 3, треугольник, шестиугольник, десятиугольник. Эти базовые модели позволяют создавать: регулярные структуры, обладающие трансляционными свойствами и подчиняющиеся законам классической кристаллографии; одномерные винтовые структуры; поверхностные структуры (плоские, цилиндрически свёрнутые и глобулярные), которые включают структуры фуллеренов и нанотрубок; квазикристаллические структуры.
При этом как бы стираются грани между кристаллами и квазикристаллами, между неорганическим и органическим веществом, т.е. формируется непротиворечивый переход от кристаллических структур, описываемых традиционной кристаллографией, к квазикристаллическим, подчиняющимся определённым математическим законам в рамках своеобразной обобщённой кристаллографии. В расширенном определении кристалла вместо элементарной ячейки, повторяющейся в пространстве строго периодическим образом, ключевым понятием становится дальний порядок. Локальная структура определяется уже не только ближайшими соседями, но и более удалёнными частицами.
Чрезвычайно важно, что именно икосаэдр (пентагондодекаэдр) является кладезем золотой пропорции. Этот эмпирический факт может быть поводом как для восторженности и культового поклонения, так и для глубокого недоверия и иронических комментариев. Такое разнополярное отношение ко всему, что связано с золотой пропорцией, мы наблюдаем у сторонников и противников икосаэдро-додекаэдрической доктрины. Концепция мировой гармонии – это философский постулат. В него можно верить или не верить, принимать или не принимать, а доказать или опровергнуть нельзя.
Эта книга не претендует на полноту изложения проблем, связанных с кристаллическим строением вещества, но, во всяком случае, всё, о чём в ней рассказано, может служить поводом для размышлений о многообразии и единстве Природы.
Публикуется с разрешения автора. Скачать полную версию (архив rar):
Информация об авторе:
Дмитрий Иванович Моисеев – инженер, кандидат технических наук, доцент.
Родился в 1935 г. в г. Ленинграде; родители: Иван Васильевич Моисеев и Татьяна Михайловна Окнова, – геологи.Житель блокадного Ленинграда.С 1951 г. проживает в г. Калининграде МО (ныне ¬– г. Королёв), пос. Болшево, дер. Бурково 16. Окончил радиотехнический факультет Московского Энергетического института в 1959 г.
10 лет работал в НИИ измерительной техники г. Калининграда МО, занимался разработкой специализированных вычислительных систем для нужд военно-космического комплекса. Затем 20 лет преподавал на кафедре Вычислительной техники Московского Лесотехнического института.Ещё 15 лет отдано системе народного образования г. Королёва: компьютеризация школ города, создание вычислительных центров в городском Комитете народного образования, в гимназии № 11, в школе-интернате для слепых и слабовидящих детей.
Всю жизнь увлекался поэзией, художественным творчеством в области деревянной скульптуры, автор многих персональных выставок в 1974 – 83 гг.
С 2001 г. целенаправленно занимается поэтическим творчеством: в 2001–2003 написан автобиографический роман в стихах "Детство, Зрелость, Юность"; в 2004 г. написана и издана книга "Благословим труды Карамзина. Древняя Русь, Киевская Русь" – стихотворное переложение "Истории Государства Российского" Н.М. Карамзина; в 2006 г. – второе, дополненное, издание: "История Руси, воспетая сонетом".
В 2007 г. написан сценарий литературно-музыкального спектакля "Человек, сотворивший себя" о жизни и творчестве Н.М. Карамзина, который поставлен театром "Трёх Муз" Людмилы Грибовой.
В 2008 г. написана книга "Человек, сотворивший себя" – стихотворное изложение биографии Н.М. Карамзина.
В связи с предстоящим в 2016 году 250-летним юбилеем Н.М. Карамзина работает над продолжением стихотворного варианта "Истории Государства Российского". Цель этой работы – популяризация творчества великого литератора и историографа, приобщение читателей к истории Отечества и необъятности, красочности русского языка.Член Союза писателей-переводчиков с 2009 г.
В течение 2010-2012 гг. написана и свёрстана научная монография "Сага об икосаэдре", посвящённая вопросам моделирования кристаллических структур.
Контактные данные: moiseevdi2011@yandex.ru
САГА ОБ ИКОСАЭДРЕ/ Моисеев Д.И.; ООО «Сен Мишель Груп», Национальный Копирайт-Центр - Москва, 2012. - 310 с. - Библиогр.: 22 назв. - Рус. - Деп. в ВИНИТИ РАН (№ 370–В2012 от 10.09.12)
Национальный Копирайт-Центр
http://nationalcenter.ru
Россия, Москва
Смоленский бульвар д. 24 стр. 2.
Группа компаний «Сен Мишель Груп»
Тел. (499) 248 28 47